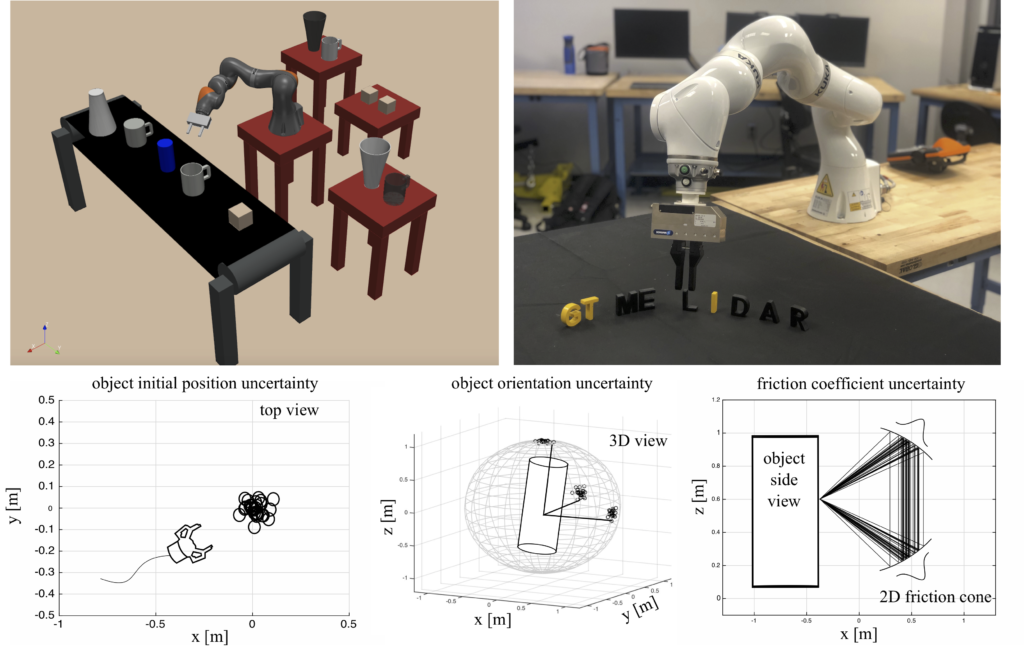
Trajectory optimization through contact is a powerful set of algorithms for designing dynamic and underactuated robot motions involving physical interaction with the environment. However, the trajectories output by these algorithms can be difficult to execute in practice due to multiple common sources of uncertainty: robot physical model errors, external disturbances, and imperfect contact surface geometry and friction estimates. To account for these uncertainties in a robust optimization framework, one typically aims to design a cost function that includes some measure of closed-loop performance variance. Unfortunately, the discontinuous nature of contact creates numerical challenges (e.g., non-differentiable cost functions, rapidly diverging trajectories) that must be addressed. We are interested in contact-physics-embedded trajectory optimization methods that employ (i) analytically quantifiable metrics and (ii) computationally efficient sampling schemes to compute a cost function that represents a local measure of trajectory variance or other risk-sensitive variants. To ensure the differentiability of the resulting cost function, we are exploring various convex approximations that can generalize the conventional linear complementarity formulation of rigid-body dynamics. The proposed robust algorithms will be evaluated in manipulating new and unforeseen objects. In particular, we are interested in manipulation tasks often observed in package sorting from logistics applications and kitchen cleaning at home. Simulations will be performed in the Drake toolbox developed by TRI while experiments will be conducted on our Kuka manipulator.
Research Challenge: what is the practically efficient way to capture uncertainties from the contact environment and robot models? Should we target a hierarchical approach (i.e., high-level task planner and low-level trajectory optimization) or a holistic approach (i.e., large-scale non-convex optimization incorporating discrete or symbolic decision variables)? Which method is more promising to enable optimization algorithm scalability?
Distributed Trajectory Optimization: Numerous prior studies on trajectory optimization rely on off-the-shelf optimization solvers or tools to solve large non-convex optimal control problems that often suffer from computational inefficiency and poor convergence rate. To alleviate these issues, we are exploiting optimization formulation structure (e.g., sparsity and convexity) and employing distributed optimization approaches for parallel computing. One example could be but not limited to the Alternating Direction Method of Multipliers (ADMM) which iteratively solves multiple decomposed sub-problems for dynamic consensus. Novel splitting schemes will be aimed for computationally efficient decomposition. The resulting multi-block optimization framework is general and has the potential to leverage the efficacy of conventional trajectory optimization methods such as (i) unconstrained optimization method–Differential Dynamical Programming, and (ii) direct methods–transcription and collocation methods. Furthermore, we are actively exploring relaxed schemes and variants to improve the overall convergence rate.
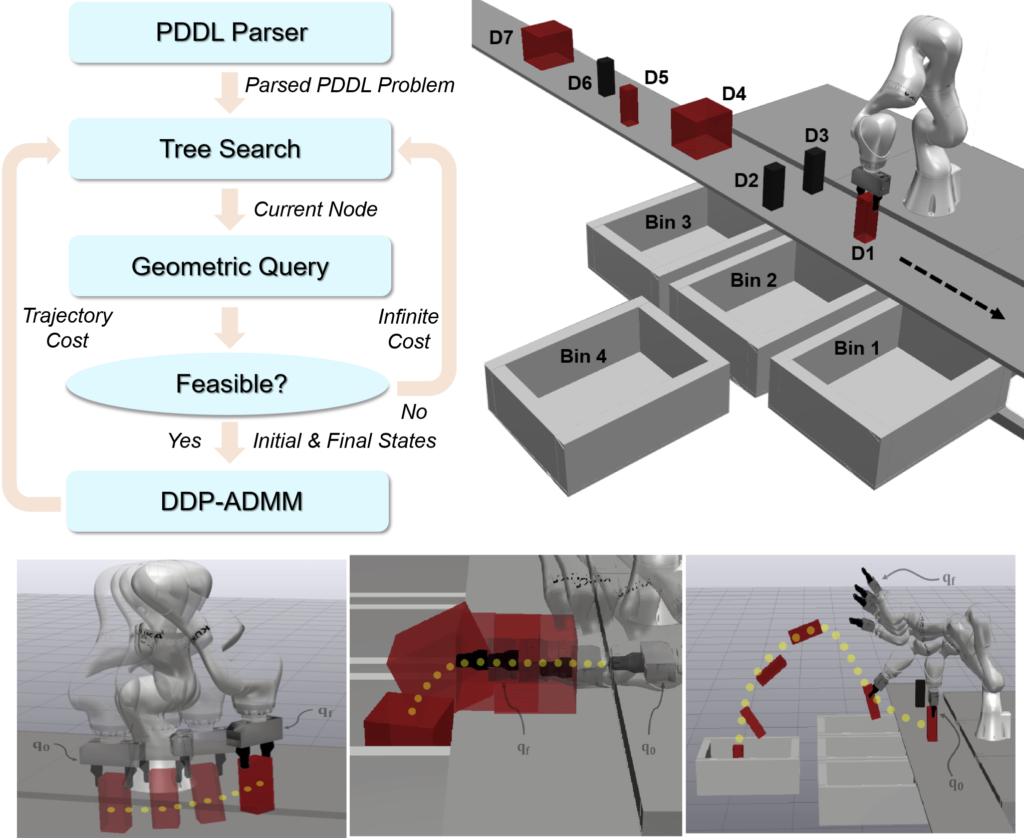
Symbolic-decision-guided Distributed Trajectory Optimization for Reactive Manipulation in Dynamic Environments: This study proposes a Task and Motion Planning (TAMP) method, where symbolic decisions are embedded in the underlying trajectory optimization and exploit the discrete structure of sequential manipulation motions for high-dimensional, reactive, and versatile tasks in dynamically changing environments. At the symbolic planning level, we propose a reactive synthesis method for finite-horizon manipulation tasks via a Planning Domain Definition Language method with A* heuristics. At the trajectory optimization level, we devise a distributed trajectory optimization approach based on the Alternating Direction Method of Multipliers, suitable for solving constrained, large-scale nonlinear optimization in a distributed manner. Distinct from conventional geometric motion planner, our approach employs Differential Dynamic Programming to solve dynamics-consistent trajectories. Furthermore, instead of a hierarchical planning approach, we solve a holistically integrated optimization simultaneously involving not only low-level trajectory optimization costs and constraints but also high-level searching and discrete costs. Simulation results demonstrate time-sensitive and responsive manipulation of sorting objects on a moving conveyor belt.
Representative publications:
Luke Drnach*, John Z. Zhang*, and Ye Zhao. Mediating between Contact Feasibility and Robustness of Trajectory Optimization through Chance Complementarity Constraints, (*equally contributed), Frontiers in Robotics and AI, 2022. [pdf] [code]
Zhigen Zhao*, Ziyi Zhou*, Michael Park, and Ye Zhao. SyDeBO: Symbolic-Decision-Embedded Bilevel Optimization for Long-Horizon Manipulation in Dynamic Environments. (*equally contributed), IEEE Access, vol. 8, pp. 12817-12826, 2021. [pdf]
Luke Drnach, and Ye Zhao. Robust Trajectory Optimization over Uncertain Terrain with Stochastic Complementarity. IEEE Robotics and Automation Letters (with ICRA option), 6(2), 1168-1175, 2021. ICRA Best Automation Paper Award Finalist [pdf] [video] [code]
Lasitha Wijayarathne, Qie Sima, Ziyi Zhou, Ye Zhao*, and Frank L. Hammond III*. Simultaneous Trajectory Optimization and Force Control with Soft Contact Mechanics. (*co-corresponding authors), IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2020. [pdf]
Z. Zhou, and Y. Zhao. Accelerated ADMM based Trajectory Optimization for Legged Locomotion with Coupled Rigid Body Dynamics, American Control Conference, 2020. [pdf]
Luke Drnach, and Ye Zhao. Robust Trajectory Optimization for Safe Locomotion over Uncertain Terrain. RSS Workshop on Robust Autonomy. 2020. [pdf] [video]
